Resonance expansion for waves on the real line

The situation changes dramatically when we consider $H_V$ with $V$ satisfying (1), on all of the real line or on a half line. The wave equation looks the same except for the lack of boundary conditions. We will assume that the initial values are zero outside some bounded set:

$$\begin{array}{c} (\partial^2_t + H_V) w(t, x) = 0, w(0, x... ... \text{ for $\vert x\vert > R_0$, for some $R_0$.} \end{array}$$ (7)

The analogue of the expansion (5) holds but with resonances in place of eigenvalues. The rôle of eigenfunctions is now played by resonant states.

To define resonant states, we make the obvious observation that any solution of

$$(H_V - \lambda^2) u = 0,$$ (8)

satisfies

$$u(x,\lambda)=\begin{cases}A_+ e^{i\lambda x} + B_- e^{-i\lamb... ...^{i\lambda x} + B_+ e^{-i\lambda x} & {\rm {for}} x \ll 0 . \end{cases}$$ (9)

The poles of the resolvent $R_V(\lambda)$, or equivalently of Green's function $G_V(\lambda, x, y)$, correspond $\lambda$'s for which the solutions satisfy

$$B_- = A_- = 0.$$ (10)

We call the corresponding solution of (8) a resonant state.

To describe the solutions of (7) in terms of resonances and resonant states let us make the simplifying assumption that the resonances are simple. That means that the poles of, say, $G_V(\lambda, x, y)$ are simple in the sense of meromorphic functions. That is the case for a generic potential [17].

The operator $H_V$ then has a finite number of negative eigenvalues,

$$E_N < E_{N - 1} < \cdots < E_1 < 0,$$

with the corresponding eigenfuctions $v_k$, and an infinite number of resonances,

$$\begin{array}{c} {\operatorname{Res}}(H_V) = \{ \lambda_j \}_{j=1... ...nfty, \ \mathop{\rm Im}\nolimits \lambda_j \rightarrow -\infty. \end{array}$$

The resonant states satisfy

$$(H_V - \lambda_j^2) u_j = 0,$$

and (10).

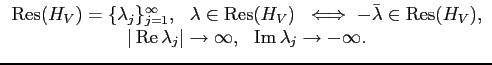
We then have the following analogue of (5) for the solutions of (7):

$$w(t,x) = \sum^N_{k=1} \cosh(t\sqrt{-E_k}) a_k v_k(x) + \sum^N_{k=1} (\sinh (t\sqrt{-E_k})/\sqrt{-E_k}) b_k v_k(x)$$

$$\quad + \sum_{-A < \mathop{\rm Im}\nolimits \lambda_j \leq 0} e^{-it \lambda_j} c_j u_j(x) + r_A(t, x) , t \rightarrow + \infty ,$$ (11)

for some constants $a_j$, $b_j$, and $c_j$, and where the error $r_A$ satisfies the following estimate for any $K > 0$:

$$\Vert r_A(t, \bullet)\Vert _{H^{k+1}([-K, K])} \leq C_{A,K,k} e^{-At} (\Vert w_0\Vert _{H^{k+1}} + \Vert w_1\Vert _{H^k} ), k \geq 0 .$$ (12)

Here $H^k$ denote the Sobolev spaces with norms,

$$\Vert u\Vert _{H^k(U)}^2 \stackrel{\rm {def}}{=} \sum_{j=0}^k \int_U \Vert \partial_x^j u(x) \vert^2 dx,$$

measuring the degree of smoothness. The estimate (12) makes sense for $k$'s for which the right hand side is finite.

Figure 2: A double barrier potential with many long lived resonances generated by squarepot([50,0,50],[-2,-1,1,2]). The imaginary parts of the first five resonances appear to be $0$ to the naked eye. They are in fact computed to be $-1.202 \times 10^{-7}$, $-9.681 \times 10^{-7}$ $-7.472 \times 10^{-6}$, $-8.864 \times 10^{-5}$, $-2.326 \times 10^{-3}$.

The expansion (11) shows that in bounded sets, such as $[-K, K]$, and for large positive times, solutions to the wave equation are desribed by modes specific to $V$ and independent of initial conditions. That is very much like the more standard (5). The waves ``resonate'' with frequencies given by $\vert\mathop{\rm Re}\nolimits \lambda_j\vert$ and decay rates given by $\vert\mathop{\rm Im}\nolimits \lambda_j\vert$.

This interpretation of resonances is quite common in popular culture, especially in the context of ``bells sounding its last dying notes''¹. An amusing example comes from Vikram Seth's beautiful translations of Li Bai's poems [28]:

A thousand valleys' rustling pines resound.
My heart was cleansed, as if in flowing water.
In bells of frost I heard the resonance die.

The word appearing in the original led to this modern translation and can be interpreted as an early (8th century) mention of resonances in literature, see also Fig.2.